Applicazioni del Teorema di Bayes: Bayesian

Il Teorema di Bayes, una formula fondamentale nella teoria della probabilità, trova applicazione in una vasta gamma di campi, influenzando la nostra comprensione e la nostra capacità di prendere decisioni in contesti incerti. Questo teorema ci permette di aggiornare le nostre credenze sulla base di nuove informazioni, consentendoci di trarre conclusioni più accurate e informate.
Applicazioni in Medicina
Il teorema di Bayes è ampiamente utilizzato in medicina per la diagnosi delle malattie. Ad esempio, un medico può utilizzare il teorema per calcolare la probabilità che un paziente abbia una certa malattia, dato che ha mostrato determinati sintomi. Questo processo, noto come diagnostica bayesiana, è diventato uno strumento fondamentale per la medicina moderna, contribuendo a migliorare l’accuratezza delle diagnosi e a ridurre i rischi di errori.
La probabilità di avere una malattia, dato che si hanno determinati sintomi, è data dal teorema di Bayes:
P(Malattia | Sintomi) = [P(Sintomi | Malattia) * P(Malattia)] / P(Sintomi)
Un esempio pratico è la diagnosi del cancro al seno. Un test mammografico può restituire un risultato positivo, ma questo non significa necessariamente che la paziente abbia il cancro. Il teorema di Bayes può essere utilizzato per calcolare la probabilità effettiva di avere il cancro, tenendo conto della prevalenza del cancro nella popolazione e dell’accuratezza del test.
Applicazioni in Finanza
Il teorema di Bayes è utilizzato in finanza per la gestione del rischio e per la previsione dei prezzi delle azioni. Ad esempio, gli analisti finanziari possono utilizzare il teorema per aggiornare le loro previsioni sui prezzi delle azioni in base a nuove informazioni, come i risultati finanziari di una società. Il teorema di Bayes può anche essere utilizzato per valutare il rischio di un investimento, tenendo conto della probabilità di diversi scenari economici.
Applicazioni nell’Intelligenza Artificiale
Il teorema di Bayes è fondamentale per l’intelligenza artificiale, in particolare per i sistemi di apprendimento automatico. Ad esempio, gli algoritmi di classificazione bayesiana utilizzano il teorema per classificare i dati in base alle loro probabilità di appartenenza a diverse categorie. Questo tipo di algoritmo è utilizzato in una varietà di applicazioni, come il riconoscimento di immagini, il filtro antispam e la previsione del comportamento dei clienti.
Applicazioni nell’Informatica, Bayesian
Il teorema di Bayes è utilizzato nell’informatica per una vasta gamma di applicazioni, tra cui il filtraggio di spam, la ricerca di informazioni e il riconoscimento di schemi. Ad esempio, i filtri antispam utilizzano il teorema di Bayes per classificare i messaggi di posta elettronica come spam o non spam, basandosi sulla presenza di determinate parole chiave o modelli.
Esempi di Problemi Risolvibili con il Teorema di Bayes
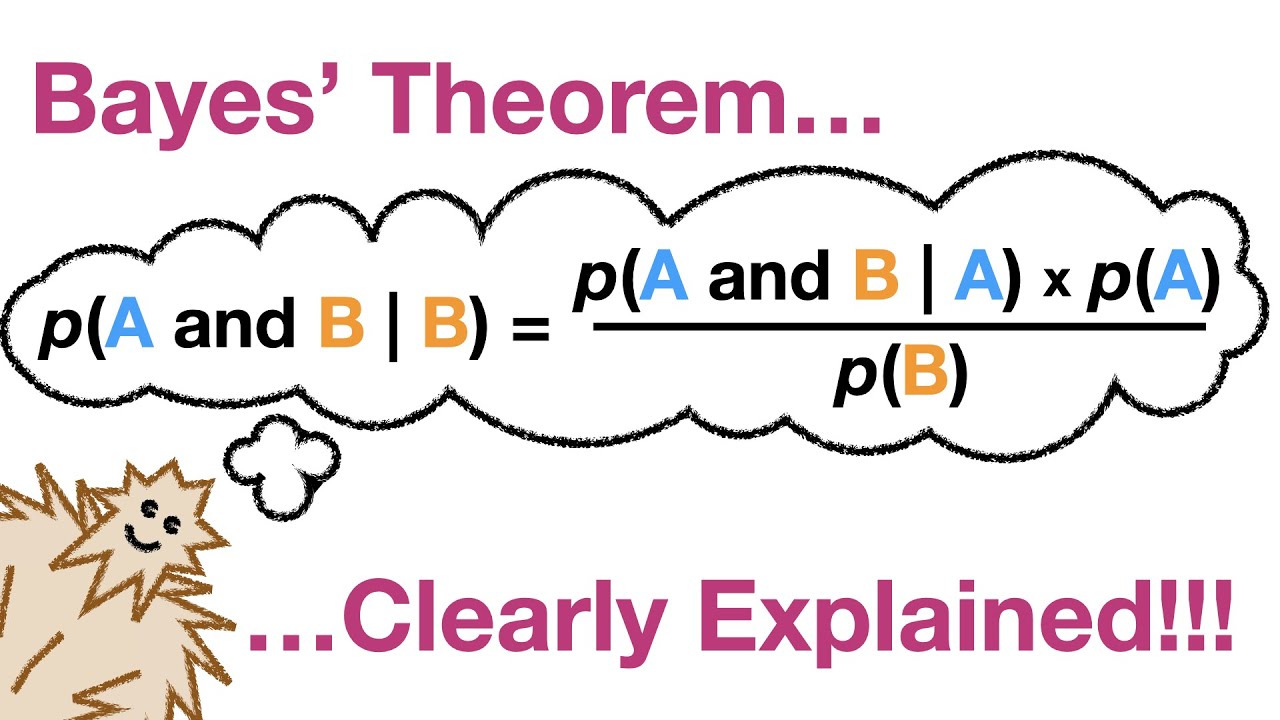
Il teorema di Bayes è uno strumento potente per risolvere problemi di probabilità condizionata. Questo teorema ci permette di aggiornare la nostra conoscenza di un evento in base a nuove informazioni. In questo modo, il teorema di Bayes è utile in diversi ambiti, come la medicina, la finanza, l’intelligenza artificiale e l’ingegneria.
Un esempio pratico: la diagnosi medica
Consideriamo un esempio pratico nel campo della medicina. Immaginiamo di avere un test per diagnosticare una malattia, come il cancro al seno. Questo test non è perfetto e può dare risultati falsi positivi o falsi negativi.
Supponiamo che il test abbia una sensibilità del 90%, ovvero che identifichi correttamente il 90% dei casi di cancro al seno. Supponiamo anche che il test abbia una specificità del 95%, ovvero che identifichi correttamente il 95% dei casi in cui la malattia è assente.
Inoltre, supponiamo che la prevalenza del cancro al seno nella popolazione sia dello 0,5%, ovvero che 1 donna su 200 abbia la malattia.
Ora, se una donna riceve un risultato positivo al test, qual è la probabilità che abbia effettivamente il cancro al seno?
Per rispondere a questa domanda, possiamo utilizzare il teorema di Bayes.
P(Cancro | Positivo) = [P(Positivo | Cancro) * P(Cancro)] / P(Positivo)
dove:
* P(Cancro | Positivo) è la probabilità di avere il cancro al seno dato un risultato positivo al test.
* P(Positivo | Cancro) è la probabilità di avere un risultato positivo al test dato che si ha il cancro al seno (sensibilità del test).
* P(Cancro) è la probabilità di avere il cancro al seno (prevalenza).
* P(Positivo) è la probabilità di avere un risultato positivo al test.
Per calcolare P(Positivo), possiamo utilizzare la legge della probabilità totale:
P(Positivo) = P(Positivo | Cancro) * P(Cancro) + P(Positivo | No Cancro) * P(No Cancro)
dove:
* P(Positivo | No Cancro) è la probabilità di avere un risultato positivo al test dato che non si ha il cancro al seno (1 – specificità).
* P(No Cancro) è la probabilità di non avere il cancro al seno (1 – prevalenza).
Sostituendo i valori noti nell’equazione di Bayes, otteniamo:
P(Cancro | Positivo) = [0.9 * 0.005] / [0.9 * 0.005 + 0.05 * 0.995] ≈ 0.082
Quindi, la probabilità che una donna abbia il cancro al seno dato un risultato positivo al test è circa l’8,2%.
Questo esempio dimostra come il teorema di Bayes può essere utilizzato per aggiornare la nostra conoscenza di un evento in base a nuove informazioni. In questo caso, il risultato positivo al test aumenta la probabilità di avere il cancro al seno, ma non la conferma.
Implementazione del teorema di Bayes in Python
Il teorema di Bayes può essere facilmente implementato in Python utilizzando la libreria `numpy`.
“`python
import numpy as np
# Definiamo le probabilità
sensibilita = 0.9
specificita = 0.95
prevalenza = 0.005
# Calcoliamo la probabilità di avere un risultato positivo al test
p_positivo = sensibilita * prevalenza + (1 – specificita) * (1 – prevalenza)
# Calcoliamo la probabilità di avere il cancro al seno dato un risultato positivo al test
p_cancro_positivo = (sensibilita * prevalenza) / p_positivo
# Stampa il risultato
print(f”La probabilità di avere il cancro al seno dato un risultato positivo al test è: p_cancro_positivo:.3f”)
“`
Questo codice produce il seguente output:
“`
La probabilità di avere il cancro al seno dato un risultato positivo al test è: 0.082
“`
Questo risultato è coerente con il calcolo manuale.
Bayesian methods, known for their ability to update beliefs based on new evidence, have found an intriguing application in the world of yachting. The concept of a bayesian yacht involves using Bayesian algorithms to optimize sailing routes, predict weather patterns, and even manage onboard systems.
This innovative approach to yachting exemplifies the versatility of Bayesian principles across diverse fields.
Bayesian statistics, a powerful tool for analyzing data, finds its application in various fields, including finance. One notable figure in the field of finance, michael lynch , has significantly contributed to the understanding of Bayesian methods in financial modeling. His work highlights the ability of Bayesian analysis to incorporate prior knowledge and uncertainty, providing a more comprehensive understanding of financial markets.
